How To Write Recursive Formula

Many elegant programming techniques exist in MATLAB, but none are quite so elegant as the recursive role. Yous create a function that keeps calling itself until a condition is satisfied, and then the function delivers an respond based on the results of all those calls. This process of the part calling itself multiple times is known every bit recursion, and a function that implements it is a recursive function.

The nigh common recursion example is computing factorial (n!), where n is a positive number. (Calculating a factorial means multiplying the number by each number below it in the hierarchy. For instance, iv! is equal to 4*3*2*1 or 24.)

Most examples that show how to create a recursive function don't actually demonstrate how the process works. The following steps help you lot create a recursive office that does demonstrate how the procedure works.

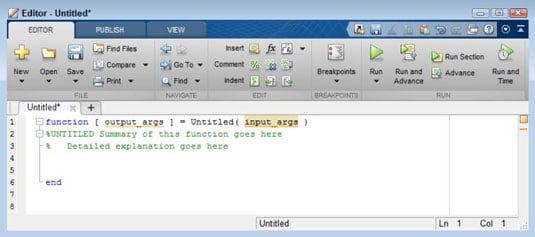
1. Click the arrow nether the New entry on the Abode tab of the MATLAB menu and select Part from the list that appears.

   Y'all come across the Editor window.

   

2. Change output_args to Event.

   The role returns a result to each preceding cycle of the call.

3. Change the function proper noun from Untitled to Factorial1.

   The master function name must match the name of the file.

4. Modify input_args to Value, Level.

   The Value received is always one less than the previous caller received. The Level demonstrates how Value is changing over time.

5. Blazon the post-obit lawmaking into the role between the annotate and the end keyword.

   if nargin < two  Level = 1; end if Value > 1  fprintf('Value = %d Level = %dn', Value, Level);  Result = Factorial1(Value - 1, Level + one) * Value;  disp(['Issue = ', num2str(Result)]); else  fprintf('Value = %d Level = %dn', Value, Level);  Effect = i;  disp(['Consequence = ', num2str(Result)]); end

   This case makes apply of an optional argument. The first time the function is called, Level won't have a value, and then the application automatically assigns it a value of ane.

   The code breaks the multiplication task into pieces. For example, when Value is 4, the code needs to multiply it past three * ii * 1. The three * 2 * 1 part of the picture is defined past the call to Factorial1(Value - 1, Level + 1).

   During the side by side pass, Value is now three. To become the appropriate result, the code must multiply this new value by 2 * 1. So, as long equally Value is greater than 1 (where an actual result is possible), the bike must go along.

   A recursive function must always accept an ending betoken — a status under which it won't call itself again. In this example, the ending point is the else clause. When Value is finally less than i, Result is assigned a value of 1 and simply returns, without calling Factorial1() again. At this betoken, the calling wheel unwinds and each level returns, one at a fourth dimension, until a last answer is reached.

   Notice that this example uses a new function, fprintf(), to display information onscreen. The fprintf() function accepts a formatting specification equally its outset input. In this case, the specification says to print the string Value =, followed by the information found in Value, then Level =, followed by the information found in Level.

   The %d in the format specification tells fprintf() to impress an integer value. You use fprintf() every bit a replacement for disp() when the output formatting starts to go more than circuitous. Notice that disp() requires the use of the num2str() part to convert the numeric value of Result to a string in order to print it.

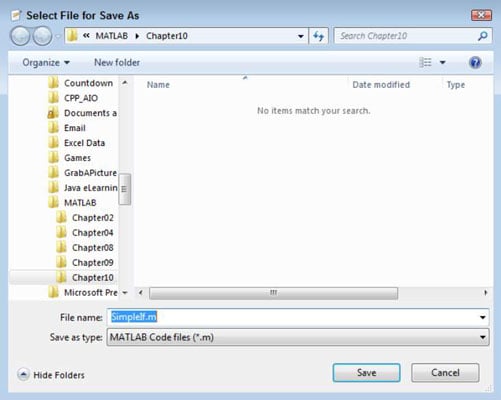
6. Click Save.

   You see the Select File for Save Equally dialog box. Notice that the File Name field has the correct filename entered for you.

   

7. Click Save.

   The function file is saved to disk.

8. Type Factorial1(four) and printing Enter in the Control window.

   You encounter the post-obit output:

   Value = 4 Level = 1 Value = three Level = ii Value = 2 Level = three Value = 1 Level = 4 Outcome = 1 Result = 2 Consequence = 6 Result = 24 ans =  24

   Notice that all the Value and Level outputs come up showtime. The function must keep calling itself until Value reaches 1. When Value does attain 1, you see the starting time Effect output. Of course, Result is likewise 1. Find how the recursion unwinds. The next Result is 2 * ane, then 3 * 2 * ane, and finally iv * 3 * 2 * 1.

Now that yous have a better idea of how the recursion works, look at the slimmed-down version.

function [ Issue ] = Factorial2( Value ) %Factorial2 - Calculates the value of n! % Outputs the factorial value of the input number.  if Value > 1  Result = Factorial2(Value - 1) * Value;  else  Event = ane;  end finish

The final version is much smaller but doesn't output any helpful information to tell you how it works. Of course, this version will run a lot faster, besides.

About This Commodity

This article is from the book:

• MATLAB For Dummies ,

About the volume authors:

John Paul Mueller is an author and technical editor with experience in awarding development, database management, automobile learning, and deep learning. He has written hundreds of books and articles helping everyday people learn everything from networking to database management.

John Mueller has produced 114 books and more than 600 articles on topics ranging from functional programming techniques to working with Amazon Spider web Services (AWS). Luca Massaron, a Google Programmer Adept (GDE),??interprets large data and transforms it into smart data through simple and effective data mining and car learning techniques.

This article can be found in the category:

• MATLAB ,

How To Write Recursive Formula,

Source: https://www.dummies.com/article/technology/programming-web-design/matlab/how-to-create-recursive-functions-in-matlab-146834/

Posted by: millermrsawas.blogspot.com

Share this post